Rete Idrica, il dimensionamento (3).

Warning: Use of undefined constant wp_hl_message_license_content - assumed 'wp_hl_message_license_content' (this will throw an Error in a future version of PHP) in D:\inetpub\webs\inambienteit\wp-content\plugins\wp-hl-message\wp-hl-message.php on line 43

Verifica alla Punta.

Per prima cosa si provvede ad eliminare le sconnessioni, così facendo si hanno come incognite: l portate, ed (n-2) quote piezometriche, conosciamo la quota piezometrica del punto di immissione A. Quindi si hanno

(1) (l + m – 2) incognite.

In compenso abbiamo proprio (l + m – 2) equazioni:

(2) yi = ± ri Qi = ± β (Q_i² / D_i⁵) l_i;
(3) Σi ± qi = 0;

purtroppo per noi, il sistema è non lineare, quindi va risolto applicando qualche risolutore. E’ tipico utilizzare, come sistema risolutore, il metodo di Hardy-Cross.

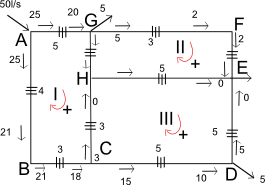
Fig 1 – Distribuzione delle portate congruenti ma non equilibrate.

Per prima cosa fissiamo le portate lungo i tratti della rete (come già sappiamo fare) rispettando la congruenza. Di norma, questo tipo di distribuzione non rispetta l’equilibrio delle maglie, cioè se andiamo ad applicate la (4) avremo un valore diverso da zero.

(4) Σ±yi =Σi± ri Qeqi² ≠ 0;  [per i = 1,…,m. Dove m: numero lati della maglia i-sima]

Ciò significa che, se andiamo a calcolare la quota piezomentrica di un punto della rete, ad esempio C, percorrendo due percorsi diversi, ad esempio AGHC ed ABC, otterremo due risultati diversi. Per rendere la distribuzione delle portate oltre che congruente anche equilibrata dobbiamo calcolare una portata correttiva [Pm] che andrà a sommarsi algebricamente alla distribuzione originaria. Dalla fig. 1, dove ho le portate non equilibrate, notiamo che se andiamo ad equilibrare la maglia I, inevitabilmente squilibriamo ulteriormente anche le maglie II e III, quindi il processo è ciclico e va ripetuto più volte.