Warning: Use of undefined constant wp_hl_message_license_content - assumed 'wp_hl_message_license_content' (this will throw an Error in a future version of PHP) in D:\inetpub\webs\inambienteit\wp-content\plugins\wp-hl-message\wp-hl-message.php on line 43
E’ inoltre ovvio che non si avrà mai un equilibrio perfetto ma faremo riferimento ad un fattore di tolleranza, ci fermeremo quando sarà verificata la (5):
(5) Pm < 2% Qin;
Dall’analisi appena fatta avremo:
(6.5) Σi ± ri (Qeqi ± Pm)²=0; poniamo ±1 = ε si ha:
(6.4) Σi ε ri (Qeqi + ε Pm)²;
(6.3) Σi ε ri (Qeqi² + 2 ε Pm Qeqi + ε² Pm²) = 0; Trascuriamo l’ultimo termine perché è un infinitesimo di ordine superiore;
(6.2) Σi ε ri (Qeqi² + 2 ε Pm Qeqi) = 0;
(6.1) Σi ε ri Qeqi² + 2 Σi ri ε ε Qeqi Pm = 0; Essendo ε² = 1 si ha:(6) Pm = – (Σi ε ri Qeqi²) / (2 Σi |ri Qeqi|); dove:
(7) ri = β li / Di5 parametri noti.
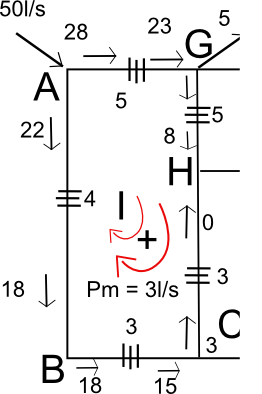
Dalla (6) ci ricaviamo la portata correttiva che andremo a sommare, considerando l’opportuno segno, ad ogni maglia della rete. Una condizione importante nell’applicazione del metodo è che la Pm, anche se da maglia a naglia può aumentare, nel complesso deve diminuire.
Dalla fig 1, se la portata correttiva fosse pari a 3 l/s avremo la situazione che vediamo nella fig 2.
Il metodo di Cross può anche funzionare considerando la portata effettivamente circolante nella rete senza far ricorso alla portata equivalente, questa trattazione, però, esula dagli obbiettivi di questi artricoli che vogliono essere una guida sintetica alla risoluzione dei problemi di dimensionamento delle reti idriche. Nel prossimo articolo vedremo la verifica a rottura di un tronco principale e la verificva all’incendio.